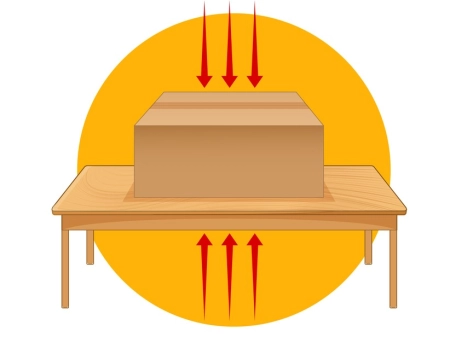
Imagine that you are sitting quietly on a chair or standing on the floor. Even if you don't think about it, a force is being produced to prevent you from falling or falling through the floor or the chair.
Have you ever wondered why, when you leave an object on a table, it doesn't go through the table and fall to the floor? This is where a "special" force comes into play in our daily life: the normal force.
In physics, this is one of the most common and essential forces, but it often goes unnoticed. It doesn't have a very flashy name, but without it, our everyday experiences would be very different.
Below I will explain what exactly this force is, how it works and why it is so important for things, including us, to stay in place.
What is normal force?
Definition
Normal force is the contact force that a surface exerts on an object when it is resting on it. This force is generated as a reaction to other forces acting on the object, such as its weight due to gravity, and is responsible for the object not passing through the surface or sinking into it.
In short, this force is the response of the surface that counteracts the forces applied to the object, keeping it in balance.
Graphic explanation
Imagine you are standing on the floor or sitting on a chair. In both cases, you are supported by a surface, right?
Well, that surface is doing something that we don't notice with the naked eye: it is pushing up against us to keep us balanced. That upward push is what we call the normal force .
It is a force that acts perpendicularly (at a right angle) to the surface on which an object is resting. This force is like the response of the surface to the weight of the object above it. The same thing happens if we leave a book on a table or if we rest our hand on a wall.
Units
Normal force , like any other force, is measured in Newtons (N).
A Newton is the standard unit of force in the International System of Units (SI), and is defined as the force required to accelerate a mass of 1 kilogram to a rate of 1 meter per second squared.
A simple example
I'll give you an example that you'll probably be familiar with: imagine you're in a park, you're sitting on a bench, and you notice how the bench supports you without you falling to the ground. What's happening?
The bench is exerting an upward force, which is the normal force , to counteract the downward force that gravity exerts on you, that is, your weight.
So when you are sitting there are two main forces at play:
- Your weight , which is the force that gravity exerts downwards.
- The normal force , which is the response of the bench pushing up.
These two forces balance each other out, which is why you don't fall through the floor or go through the bench. So basically, the normal force is responsible for keeping us from sinking into things!
Why is it called "normal"?
The word "normal" in this case has nothing to do with what we use in everyday life (like when we say "that's normal" or "this is weird"). Here, "normal" means perpendicular.
It is a mathematical term used in physics to refer to a specific direction that forms a 90-degree angle with a surface.
So when we say "normal force," we're talking about a force that always points in that direction, outward and perpendicular to the surface.
How exactly does it work?
Now that we understand the basics, let's dig a little deeper into how the normal force works. This force doesn't have a fixed value. It doesn't always push upward with the same intensity. Its value depends on several factors, and one of the most important is the weight of the object .
Imagine that you drop a book on a table. The force that the book exerts on the table is the weight of the book, which is the force of gravity pulling downward. In response, the table exerts an upward force, equal in magnitude to the weight.
If the book weighs 2 kilograms, the table will push upwards with a force equal to the weight of the book. But if you add more books on top, the force exerted by the (normal) table will have to increase to continue to support the extra weight.
It should be noted that if there are other forces in addition to weight, these also intervene in the normal force. For example, if we push the book downwards with our hand, the normal force will be the sum of the weight plus the force that we exert downwards.
Calculating normal force with formulas
We distinguish two special cases: when the object is on a horizontal surface and when it is on an inclined plane.
Calculation on a horizontal surface
The basic formula for calculating normal force, in situations where the object is on a horizontal surface with no inclinations or extra forces, is quite simple:
F n = m⋅g
Where:
- m is the mass of the object in kilograms (kg).
- g is the acceleration of gravity, which on Earth is approximately 9.8 m/s2.
For example, if you have an object that weighs 10 kg, its weight would be:
Weight=10 kg⋅9.8 m/s 2 =98N
And the normal force would also be 98 Newtons (N), because the surface has to exert an equal and opposite force to hold the object in balance.
Calculation on an inclined plane
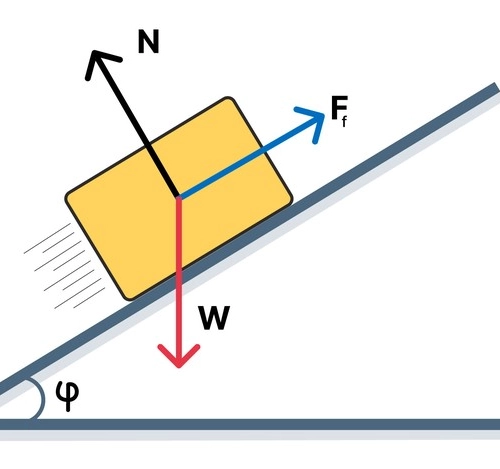Now let's see how it is calculated when an object is on an inclined plane. This is a bit more complicated than on a flat surface, because not all of the force of the object's weight is acting directly against the surface, as some of that force is "sliding" down along the slope.
When you place an object on an inclined surface (such as a ramp or hill), its weight still acts downward due to gravity, but it is broken down into two components:
- A component parallel to the inclined surface: This is the part of the weight that "pushes" the object down along the slope, which is why objects can slide on a ramp.
- A component perpendicular to the inclined surface: this is the part of the weight that "presses" directly against the ramp, and this is what generates the normal force.
Let's see how it is calculated in this case.
Weight decomposition on an inclined plane
To calculate the normal force on an inclined plane, the first thing we have to do is break down the force of gravity into these two parts that I mentioned before: one parallel and one perpendicular.
If the angle of inclination of the ramp is θ (the angle between the inclined surface and the flat ground), we can use trigonometry to calculate each of those components.
The total weight of the object is:
Weight=m⋅g
Where m is the mass of the object and g is the acceleration due to gravity (approximately 9.8 m/s 2 ).
- Perpendicular component (which is the one that generates the normal force):
This is the part that interests us, because it is the one that "rests" on the ramp and is related to the normal force. The formula to calculate this component is:
F⊥=m⋅g⋅cos(θ)
Here, cos(θ) is the cosine of the angle of inclination. - Parallel component (which makes the object tend to slide):
It does not directly affect the normal force, but it is useful to know it to understand the movement of the object on the ramp. It is calculated like this:
F∥=m⋅g⋅sin(θ)
Calculation of normal force
Once we have broken down the weight into these two parts, we can calculate the normal force (F n ) . The F n on an inclined plane will be equal to the perpendicular component of the force of gravity, since it is this that the surface of the ramp has to counteract.
Therefore, the normal force is:
F n = m⋅g⋅cos(θ)
Practical example
Imagine that you have a 5 kg block placed on a ramp inclined at 30 degrees to the ground. We want to calculate the normal force exerted by the ramp on the block.
First, we calculate the weight of the block:
Weight=5 kg⋅9.8 m/s2=49 N
Now we use the formula, with the inclination angle of 30 degrees:
Fnormal=49 N⋅cos(30∘)
The cosine of 30 degrees is approximately 0.866, so:
Fnormal=49 N⋅0.866=42.4 N
Therefore, the normal force that the ramp exerts on the block is 42.4 Newtons .
Why is it smaller than on a flat surface?
Note that the normal force on an inclined ramp is less than if the same block were on a flat surface. If the block were on a horizontal surface (where the angle θ is 0 degrees), the cosine of 0 is 1, so the normal force would be equal to the entire weight, or 49 N.
In the case of the ramp, since the angle of inclination is 30 degrees, only part of the weight is being "supported" on the ramp, and that is why the normal force is less, 42.4 N instead of the 49 N that we would have on a flat surface.
The other component of the force is the one that would cause a downward acceleration of the body unless there was a friction force in the opposite direction to compensate it.
This also explains why it is easier for an object to slide down an inclined slope: since the normal force is smaller, there is less friction, and the part of the weight acting down the slope (the parallel component) helps the object move.
Special situations
So far we have talked about very simple examples, but this force can also behave in interesting ways in more complex situations.
Below are some special examples that will help you better understand this concept:
1. Earrings
Imagine you are walking up a steep hill. Have you noticed that it is easier to slip on a slope? This has to do with the normal force.
When an object is on an inclined surface, the normal force is not as large as when the surface is flat, because the inclination causes part of the gravitational force to act "pushing" down the slope.
On a hill, the normal force doesn't have to offset the entire weight of the object, only part of it. And because it's smaller, there's less resistance and it's easier for you to slip.
2. Pushing against a wall
Now, imagine you are pushing a box against a wall.
In this case, the normal force is not related to the weight of the box, but to the pressure you are exerting. The harder you push the box against the wall, the greater the force the wall will exert on the box to prevent it from passing through.
If you stop pushing, the normal force disappears.
3. Normal force on an elevator
Have you ever felt like you weigh more or less in a moving elevator?
This also has to do with this type of force. If the elevator goes up at an accelerated rate, the normal force increases (and we feel as if we weigh more), because the floor of the elevator has to push upwards with greater force to compensate for the acceleration.
If the elevator accelerates downwards, the normal force decreases (and we feel like we weigh less), because the acceleration reduces the need to push upwards as hard.
Relationship with Newton's third law: action and reaction
The normal force is directly related to Newton's third law , also known as the law of action and reaction .
This law states that for every action, there is a reaction of equal magnitude and in the opposite direction . That is, if one object exerts a force on another, that other object responds with an equal force but in the opposite direction.
In the case of the normal force, imagine a skater gliding across an ice rink. The skater's weight, which is the action force , pushes downward due to gravity.
In response, the ice exerts an upward force to counteract this weight and prevent it from breaking and the skater from passing through. The magnitude of this force is equal to the skater's weight, but it acts in the opposite direction, that is, upwards.
Conclusion
In short, normal force is one of those things that is present all the time, but we usually don't realize it exists.
It is the force that prevents us from passing through the ground or objects from sinking into surfaces. It depends on the weight of the object and always acts perpendicular to the surface on which it is resting. In addition, it is involved in all kinds of everyday situations, from sitting to walking up a slope.