Bernoulli's equation is one of the basic principles of physics and engineering that describes the relationship between the velocity of a fluid and its pressure. This principle is crucial in understanding fluid mechanics and is used in areas ranging from aerodynamics, hydrodynamics, and bridge engineering.
Bernoulli's principle is an expression of the law of conservation of energy for an incompressible fluid in a steady state. Torricelli's theorem is a consequence of this principle.
What does Bernoulli's principle say?
Bernoulli's principle states that the sum of static pressure, dynamic pressure, and velocity pressure in an incompressible fluid is constant along a flow line.
In other words, if the speed of a fluid increases, its pressure will decrease and vice versa. This principle can be expressed mathematically by the Bernoulli equation, which relates the pressure, speed and height of a fluid at a given point.
Bernoulli equation
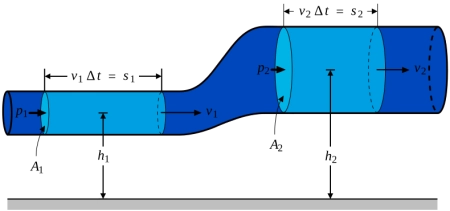
The Bernoulli equation in mathematical terms is expressed as follows:
P + 1/2·ρ·v 2 + ρ·g·h = constant
Where:
- P is the static pressure of the fluid at the point considered.
- ρ is the density of the fluid.
- v is the velocity of the fluid at the point considered.
- g is the acceleration due to gravity.
- h is the height of the point considered with respect to a reference level.
La constante en la ecuación representa la suma de las presiones en otro punto de la línea de flujo, y su valor se mantiene constante en cualquier punto a lo largo de la línea de flujo.
It is important to note that Bernoulli's equation is only applicable in certain situations, such as in incompressible fluids, in steady state, and along a flow line. In addition, the equation does not take into account factors such as fluid viscosity or the presence of turbulence, so it may not be applicable in all situations.
What is the Bernoulli equation used for?
The Bernoulli equation is a fundamental tool in fluid mechanics and is used to describe the behavior of fluids in a wide variety of practical situations.
Important applications of Bernoulli's equation include:
- Pipe and duct design: Bernoulli's equation is used to calculate the pressure and velocity of fluid flow in pipes and ducts, which is fundamental in civil and mechanical engineering.
- Wing Design and Aerodynamics: Bernoulli's principle is applied in the design of aircraft wings and other aerodynamic devices. The shape of the wings is designed to create a pressure difference between the top and bottom of the wings, which allows the aircraft to fly.
- Hydraulics and Pneumatics: Along with Pascal's principle, this equation is used to design hydraulic and pneumatic systems used in industrial machinery design.
- Flow Measurements: This equation is also used to measure fluid flow in a wide variety of applications, such as measuring water flow in a pipe or air flow in a duct.
Examples of Bernoulli's principle
There are several experiments that can be performed to demonstrate Bernoulli's principle and how velocity and pressure are related in an incompressible fluid. Some examples of Bernoulli experiments are:
airplane wing
The design of an airplane wing is based on Bernoulli's equation. The curved shape of the wing causes the air flowing above the wing to move faster than the air flowing below the wing.
This creates a low pressure area on the top of the wing and a high pressure area on the bottom of the wing, which generates an upward force (lift) that compensates for the aircraft's own weight.
Venturi tube
The Venturi tube is a device used to measure the velocity of a fluid. The tube consists of a conical section that narrows in the center, causing an increase in the velocity of the fluid as it passes through the narrower section.
As the velocity of the fluid increases, the pressure decreases according to Bernoulli's principle. The pressure difference can be measured using a pressure gauge, allowing the velocity of the fluid to be calculated.
Ping-pong ball
If a ping-pong ball is held in a jet of air, the ball will remain suspended in the air due to the Coandă effect. This is an ideal example to show how Bernoulli's principle works using the scientific method.
Air moves faster around the ball than under it, causing a decrease in pressure at the top of the ball, which causes the ball to be pushed upward.