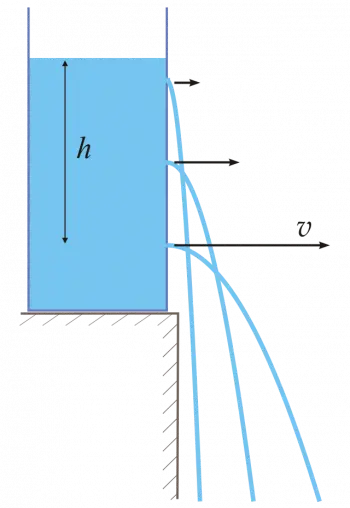
Torricelli's theorem is a principle of fluid mechanics that studies the behavior of a fluid in a container with a hole. For this reason, it is also known as Torricelli's principle.
Torricelli's principle is used in hydraulics and fluid dynamics to determine the flow rate of a liquid through an orifice. In general, Torricelli's law can be applied in various fields, including civil engineering, hydrology, physics, and meteorology, among others.
This principle was stated by the Italian physicist and mathematician Evangelista Torricelli in the 17th century.
Definition of Torricelli's theorem
Torricelli's principle states that the speed of a liquid flowing through the hole in a container is equal to the speed of a body falling freely from a height equal to the distance from the liquid level to the center of gravity of the hole.
The characteristics of the fluid for the theorem to be valid are that the fluid must be incompressible, with zero viscosity and must be subject only to the gravitational force.
This theorem is based on the law of conservation of mechanical energy, which states that the total energy of a closed system is conserved. Specifically, it is a consequence of Bernoulli's principle.
Torricelli's equation
Torricelli's equation describes the velocity of a fluid flowing through an orifice due to the height difference between the fluid in the container and the outlet. It is a derivative of the law of conservation of energy and is expressed as follows:
\[
v = \sqrt{2gh}
\]
Where:
- \( v \) is the exit velocity of the fluid (in meters per second).
- \( g \) is the acceleration due to gravity (approximately \( 9.81 \, \text{m/s}^2 \)).
- \( h \) is the height of the fluid in the container above the level of the outlet orifice (in meters).
Explanation:
- Torricelli's principle states that the speed with which a fluid leaves a container is equivalent to the speed that an object would have if it fell freely from a height h (due to the action of gravity).
- The equation is based on the conversion of the potential energy of the fluid (due to its height) into kinetic energy (due to the exit velocity).
This equation is valid under the assumption that the flow is ideal, with no friction losses or other complicating factors.
Examples of Torricelli's principle
Torricelli's principle can be observed in a wide variety of practical situations. Some examples are presented below:
Pitot tube
The Pitot tube is an instrument used to measure the velocity of fluids, such as air in aircraft or liquids in pipes.
It consists of two tubes: one measures static pressure (the pressure exerted uniformly by the fluid), while the other measures total pressure (which includes dynamic pressure due to fluid motion). The difference between these two pressures is used to calculate the fluid's velocity, applying Torricelli's principle. This device is used in aeronautics to determine aircraft speed and is also used in engineering to evaluate flow in hydraulic systems.
Ornamental fountains and water jets
Water fountains, especially ornamental ones, use Torricelli's principle to generate jets of water through a nozzle.
The velocity of the water emerging from the fountain is directly related to the height of the water in the reservoir that feeds it. The greater the height of the water, the greater the pressure at the base, which increases the flow velocity through the nozzle.
This principle is used not only in decorative fountains, but also in irrigation systems and in natural phenomena such as geysers, where the pressure of hot water pushes the liquid upward.
Filling bottles and containers
When a liquid is poured from a large container into a bottle or glass, the flow of liquid is influenced by the difference in height between the liquid levels in both containers.
Initially, the flow is rapid due to the high pressure generated by the liquid in the large container. However, as the liquid level in the large container decreases, the pressure decreases, causing the flow to slow down. This behavior is explained by Torricelli's principle, which states that the velocity of the fluid at the orifice depends on the height of the liquid column.
Draining tanks and reservoirs
Torricelli's principle also applies to the drainage of liquids from tanks or reservoirs.
When a liquid flows from a tank through a valve or orifice at the bottom, the rate at which the liquid exits is determined by the height difference between the liquid level in the tank and the outlet. The greater this height difference, the greater the flow rate, allowing the tank to be emptied more quickly.
This phenomenon is observed in systems such as water tanks, storage towers, and drainage systems.
Holes in perforated containers
When a container filled with water has a hole in its sidewall, the water begins to flow outward due to the internal pressure exerted by the liquid in the container. According to Torricelli's principle, the speed with which water flows out of the hole depends on the height of the water level in the container relative to the hole.
The higher the height, the greater the velocity of the water as it exits. This phenomenon can be observed in physics experiments to illustrate how pressure and gravity influence the flow of liquids, and it occurs in everyday situations, such as when a container of water has a small hole in its side.
Torricelli's experiment
The Torricelli experiment, carried out in 1643 by the physicist and mathematician Evangelista Torricelli, demonstrated the existence of atmospheric pressure and was key to the invention of the barometer.
Description of the experiment
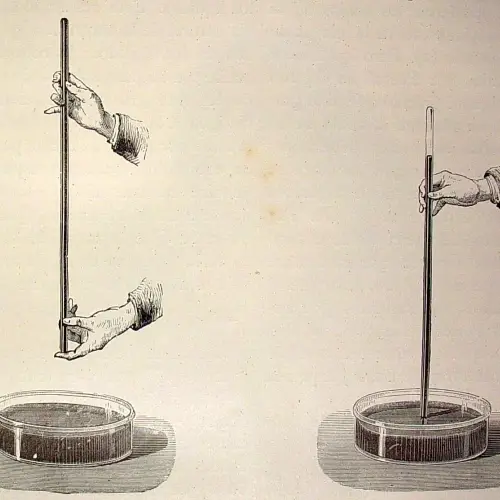Torricelli filled a glass tube about a meter high with mercury and covered it with his finger. He then inverted the tube and immersed it in a container also filled with mercury.
Upon removing his finger, he observed that the level of mercury in the tube decreased, but did not empty completely, leaving approximately 76 cm of mercury inside the tube.
Conclusion
- Torricelli deduced that the mercury did not fall completely because atmospheric pressure pushed the mercury into the container, balancing its weight inside the tube.
- At the top of the tube, an empty space (called a "Torricellian vacuum") remained, which was one of the first experimental evidence of vacuum in nature.
- He determined that atmospheric pressure could be measured by the height of the mercury in the tube, establishing the basis of the first barometer.
This experiment provided a better understanding of air pressure and laid the foundation for the development of meteorology and fluid physics.
Practical experiment with a bottle of Torricelli's principle
Below, we show a very simple experiment to illustrate how Torricelli's theorem works, which can also be used to explain the scientific method. This experiment can be done with materials found around the house.
Materials:
- An empty plastic bottle
- A sharp nail or needle
- Water
Instructions:
- Fill the plastic bottle halfway with water.
- Pierce a small hole about halfway through the bottle with the nail or needle.
- Place a container under the bottle to collect the water that comes out through the hole.
- Open the bottle cap to allow air to enter and water to flow smoothly.
Observations:
When the hole is made in the bottle, water begins to flow through the hole. The velocity of the water decreases as more water leaves the bottle. The water particles exiting the hole follow the typical trajectory of a parabolic shot with an initial horizontal velocity.
Knowing the height of the hole relative to the surface of the container where the water falls and the horizontal distance from the hole to the point where the water falls, we can calculate the exit velocity of the water at any instant.