Uniform circular motion (UCM) is a fundamental concept in kinematics that describes a specific type of motion in which an object moves around a fixed point in a circular path at a constant speed.
In this article, we will define the MCU, and the different basic concepts related to this movement, some real examples that illustrate this movement, the formulas for its calculation and we will solve some exercises to understand it better.
Definition of uniform circular motion (MCU)
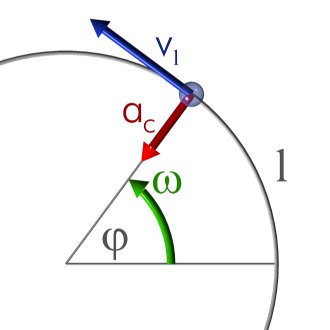Uniform circular motion (UCM) is a specific type of motion in which an object moves around a fixed point in a circular path at a constant speed.
In the MCU, the velocity of the object remains unchanged in magnitude and direction throughout its path, meaning that the angular velocity is constant.
Uniform circular motion is characterized by the relationship between angular velocity and linear velocity, which is directly related to the radius of the circular path.
This motion is typically observed in situations such as the orbit of a planet around a star, the turning of a wheel on a moving vehicle, or even in roller coaster amusement parks, where passengers experience a constant sensation of speed and direction as they rotate around a central point.
Uniform circular motion basics
To understand the MCU, it is essential to familiarize yourself with some key concepts:
1. Period (T) and frequency (f)
The period (T) is the time it takes for the object to complete one complete revolution around the circular path. The frequency (f) is the number of revolutions that the object completes in one second. They are related as follows:
f = 1/T
In the International System of Units (SI), period is measured in seconds (s). On the other hand, frequency is measured in hertz (Hz). One hertz is equal to one cycle per second.
2. Angular velocity (ω)
Angular velocity (ω) is a measure of how fast the object is moving around the circular path. It is measured in radians per second (rad/s) and is related to frequency (f) as follows:
ω = 2·π·f
3. Radius of the path (r)
The path radius (r) is the distance from the center point to the moving object in the MCU. This value is constant throughout the movement.
4. Linear speed (v)
Linear velocity (v) is the speed with which the object moves tangentially along the circular path. For this reason it is also known as tangential velocity.
Tangential velocity is related to angular velocity (ω) and radius (r) as follows:
v = r·ω
5. Centripetal acceleration (ac )
Centripetal acceleration (ac ) is a fictitious acceleration that acts on the object in a direction opposite to the center of the circular path. Its magnitude is related to the angular velocity (ω) and the radius (r) as follows:
ac =r·ω 2
The units of centripetal acceleration are meters per second squared (m/s²).
Formulas for uniform circular motion
The following formulas are essential for understanding and solving problems related to the MCU:
-
Relationship between angular velocity and linear velocity: v=rω
-
Relationship between period and frequency:T=1/f
-
Relationship between angular velocity and frequency: ω=2πf
-
Relationship between centripetal acceleration, angular velocity and radius: a c =rω 2
Examples in everyday life
Uniform circular motion is found in numerous aspects of everyday life.
-
Steam turbines in nuclear power plants: Steam turbines in nuclear power plants use the MCU to convert thermal energy into mechanical energy, generating electricity.
-
Ceiling Fans: Ceiling fan blades perform an MCU to circulate air evenly in a room, providing cooling.
-
Vehicles on curves: Vehicles, when turning on circular curves, follow a MCU that can be calculated using these formulas.
-
Rope Making: Twisting a rope to create a rope involves an MCU, where the rope is wound evenly around a central core.
Solved exercises
Now, let's solve some typical exercises related to the MCU:
Exercise 1
Suppose a racing car moves at a constant speed of 100 m/s around a circular track of radius 200 meters. Calculate the period, frequency and angular velocity of the motion.
Solution:
Since the velocity is constant, we can use the formula for angular velocity:
v = r·ω
Substituting known values:
100 m/s = 200 m ⋅ ω
To find ω:
ω = (100 m/s) / 200 m=0.5 rad/s
Now, we can find the period (T) using the relationship between angular velocity and frequency:
ω = 2·π·f
0.5 rad/s = 2·π⋅f
To find f:
f = (0.5 rad/s) / (2·π) ≈ 0.0796 Hz
And finally, the period (T) is the reciprocal of the frequency:
T = 1/f ≈ 12.57 s
Exercise 2
An object moves along a circular path of radius 4 meters at an angular velocity of 2 radians per second. Calculate its linear velocity and centripetal acceleration.
Solution:
To find the linear velocity, we use the formula:
v = r·ω
Substituting known values:
v=4m ⋅ 2 rad/s = 8 m/s
For centripetal acceleration, we use the formula:
ac = r·ω2
Substituting known values:
ac = 4 m⋅(2 rad/s)2 = 16 m/s2