Uniformly accelerated circular motion (UACM) is a type of motion in which an object moves along a circular path with a constant acceleration.
The MCUA is a type of movement crucial in calculating the kinematics of a body. This phenomenon is fundamental to understanding a wide range of situations, from vehicle mechanics to the dynamics of orbiting planets, and can be described by specific formulas that relate angular velocity, angular acceleration, and time.
What is uniformly accelerated circular motion?
Uniformly accelerated circular motion (UACM) is a fundamental concept in physics that describes the motion of an object along a circular path with a constant acceleration.
Unlike rectilinear motion, in which an object moves in a straight line, MCUA involves a constant variation in the angular velocity of the object, causing it to rotate along a closed curve.
In the MCUA, the angular acceleration of the object is constant, meaning that its angular velocity increases or decreases uniformly with time.
Basic characteristics of the movement
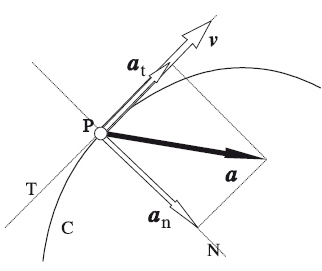The basic characteristics that define this movement are:
- The object moves in a circular path. This implies the appearance of a centripetal acceleration to keep the distance of the object from the center of rotation constant.
- Angular velocity undergoes a constant angular acceleration, therefore, tangential velocity also undergoes a tangential acceleration.
Basic concepts
Angular velocity
Angular velocity, represented by the Greek letter "ω" (omega), is a measure of how quickly an object rotates along the circular path. It is measured in radians per second (rad/s).
Tangential speed
Tangential velocity is the linear velocity of an object at a specific point on its circular path. It refers to the magnitude of the velocity of an object in a direction tangent to the curve at that point.
Angular acceleration
Angular acceleration, represented by "α" (alpha), is the change in angular velocity per unit time. Like angular velocity, it is measured in radians per second squared (rad/s²).
Centripetal acceleration
Centripetal acceleration is an acceleration directed toward the center of a circular path. It occurs when an object moves in a curved orbit and experiences a constant change in the direction of its speed without affecting its magnitude.
Tangential acceleration
Tangential acceleration is a measure of how the magnitude of the speed of a moving object changes along a curved path. This acceleration occurs when the tangential speed of the object varies.
Calculation formulas
Formula for angular velocity as a function of time
The relationship between initial angular velocity (ω₀), angular acceleration (α) and time (t) can be described by the following formula:
ω= ω₀ + α·t
Where
- ω is the final angular velocity.
- ω₀ is the initial angular velocity.
- α is the angular acceleration.
- t is time
Rotated angle formula
The amount of angle rotated (θ) at a time "t" is related to the angular velocity and angular acceleration as follows:
θ = ω₀·t + ½·α·t²
Where
- θ is the rotated angle.
- ω₀ is the initial angular velocity.
- α is the angular acceleration.
- t is time
Formula for angular velocity as a function of angular velocity
The final angular velocity (ω) is related to the initial angular velocity, the angular acceleration and the rotated angle by the following formula:
ω² = ω₀² + 2·α·θ
Where
- ω is the final angular velocity.
- θ is the rotated angle.
- ω₀ is the initial angular velocity.
- α is the angular acceleration
Illustrative everyday examples
Uniformly accelerated circular motion (UACM) is found in numerous aspects of everyday life and in various contexts, some examples include:
- Clothes Washer: In the spin cycle, clothes spin in the drum with a constant acceleration, allowing water to be expelled out.
- Fairground rides: Fairground rides, such as Ferris wheels and carousels, apply a start-stop MCUA to allow passengers to get on and off.
- Wind turbines: windmills suffer a MCUA when they start up or when there are variations in wind intensity.
- Steam turbines: The turbines of a nuclear power plant are optimized to rotate at a constant speed. While uniformly accelerated circular motion occurs during starting and stopping, its efficiency is lower.
Solved exercises
Exercise 1: Rotation of a fan
A fan rotates with an initial angular velocity of 3 rad/s and experiences an angular acceleration of 0.5 rad/s². How long will it take to reach an angular velocity of 7 rad/s?
Solution
We use the formula for the final angular velocity:
ω = ω₀ + αt
We substitute the known values:
7 rad/s = 3 rad/s + (0.5 rad/s²) t
We solve for you:
(0.5 rad/s²)t = 7rad/s − 3 rad/s
0.5t = 4 rad/s
t=(4 rad/s) / (0.5 rad/s²) = 8 s
The fan will take 8 s to reach an angular velocity of 7 rad/s.
Exercise 2: Spin of a Ferris wheel
A ferris wheel begins to rotate from rest with an angular acceleration of 0.8 rad/s². How long will it take for the ferris wheel to turn 5 radians?
Solution
We use the formula for the rotated angle:
θ = ω₀t + ½·α·t²
We substitute the known values:
5rad = (0 rad/s)·t + ½(0.8 rad/s²)·t²
We simplify the equation:
5rad = (0.4 rad/s²)t²
We solve for you:
t = √( 5 rad / 0.4 rad/s²)
t ≈ 3.54s
The Ferris wheel will take approximately 3.54s to rotate 5 radians from rest.