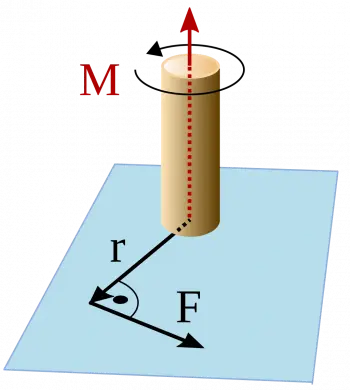
The moment of a force, also known as "torque", is a physical quantity that measures the tendency of a force to rotate an object around a point or axis of rotation.
The moment of a force is related to Newton's laws because the magnitude of the applied force affects the angular acceleration of the object (second law) and because the moment generated by the force on an object also generates an equal but opposite force on the object. direction of the axis of rotation or on another object (third law).
Mathematically, the moment of a force is defined as the product of the value of the force (F) and the perpendicular distance (r) from the point of application of the force to the axis of rotation.
The moment of a force can be calculated in different situations, either in the context of an object at rest (static) or in motion (dynamic).
Formula for the moment of a force
The formula to calculate the moment (τ) of a force (F) with respect to a point or axis of rotation, taking into account the perpendicular distance (r) from the point of application of the force to the axis of rotation, is as follows:
Moment (τ) = F × r
Where:
-
τ = Moment of force (torque) in units of newton meters (Nm) or foot-pounds (lb-ft)
-
F = Magnitude of the applied force, measured in newtons (N) or pounds (lb)
-
r = Perpendicular distance from the point of application of the force to the axis of rotation, measured in meters (m) or feet (ft)
This formula applies when the force and distance are perpendicular to each other, which means that the force acts in a direction that makes an angle of 90 degrees to the radius or distance from the axis of rotation.
In situations where the force and distance are not perpendicular, it is necessary to use concepts of vectors or trigonometry to resolve the force into its components perpendicular to the radius, which will allow the resultant moment to be calculated.
If done in terms of vectors, the direction of momentum follows either the right-hand rule or the corkscrew rule, depending on the convention. This implies that the moment can be positive or negative depending on the direction in which the force acts relative to the axis of rotation.
Examples
The moment of a force has common applications in our daily life in various situations. Here are some examples of how the moment of a force is applied in everyday life:
-
Opening Doors: When you turn a door handle to open it, you are applying a moment on the hinges. The further the applied force is from the hinges, the easier it will be to open the door, since the moment will increase and it will require less force to turn.
-
Tightening bolts: When you use a wrench to tighten a bolt, you apply a moment about the axis of the bolt. The length of the wrench (distance from the axis of the screw) influences the amount of force you need to apply to successfully tighten the screw.
-
Turning a Wrench: When you use a wrench to loosen or tighten nuts and bolts, you are applying a moment about the axis of the bolt. Again, the length of the wrench determines the amount of moment that is generated and therefore the ease of turning the nut or bolt.
-
Car steering wheel: When you turn a car steering wheel to change direction, you apply a moment about the vehicle's steering axis. The further you turn the steering wheel from the steering axis, the faster the direction of the car will change.
-
Swinging on a swing: When you swing, you apply momentum around the hooks of the swing. By pushing your feet back and forth while sitting on the swing, you control the momentum and determine the range and speed of the movement.
-
Bicycle: when applying a force to the pedals of a bicycle, it generates a moment of forces with respect to the axis of the pedals. Likewise, the force that is transmitted to the chain depends directly on the radius of the chainrings, which is the distance from the center of rotation.
-
Lever: A lever is a simple machine consisting of a rigid bar that pivots about a fixed point called the fulcrum. By applying a force to one end of the lever (input force), a moment is generated that allows a load to be lifted at the other end (output force).
-
Pulley: A pulley is a wheel with a rope or cable running through it. Pulling on one end of the rope (input force) applies a moment on the pulley, allowing a load to be lifted at the other end (output force).
-
Steam turbine: the steam turbines used in the electrical generators of a nuclear power plant are designed so that the steam generates a tangential force to the wheel and perpendicular to the axis in such a way that it generates a moment of forces to obtain a circular movement.
Solved exercises
Exercise 1: Moment of a force perpendicular to the axis of rotation
Suppose we have a door that rotates around its hinges, and we apply a force of 20 newtons in the direction perpendicular to the axis of rotation, at a distance of 0.5 meters from the axis of rotation to the point of application of the force. Calculate the moment of force.
Solution
The moment of force would be calculated as follows:
Moment (τ) = F × r
τ = 20 N × 0.5 m
τ = 10 Nm
The moment of force applied to the door is 10 newton meters (Nm).
Exercise 2: Moment of a force not perpendicular to the axis of rotation
Now suppose we apply a force of 30 newtons to the same door, but this time the force acts at an angle of 60 degrees to the axis of rotation, and the distance from the axis of rotation to the point of application of the force is 1 meter. Calculate the moment of force.
Solution
To calculate the moment, we must first resolve the force into its components perpendicular to the radius.
Force perpendicular to radius (Fperpendicular ) = F × cos(θ)
Fperpendicular = 30 N × cos(60°)
Fperpendicular = 30 N × 0.5
Fperpendicular = 15 N
Moment (τ) = Fperpendicular × r
τ = 15 N × 1 m
τ = 15 Nm
The moment of the force applied to the door, considering its component perpendicular to the radius, is 15 newton meters (Nm).