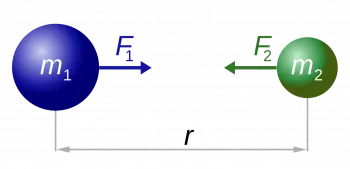
Newton's universal law of gravitation is one of the fundamental pillars of physics and was developed by Sir Isaac Newton in the 17th century. This law describes the force of attraction between two bodies due to their mass and relative distance.
It is one of the most important and widely applied laws in the field of classical physics and has made it possible to understand and predict many phenomena in the universe.
In this article, we will explore in detail what the universal law of gravitation is, its formula, its importance, and some examples that illustrate its application.
What is the universal law of gravitation?
The universal law of gravitation establishes that the force of attraction between two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance that separates them.
That is, the greater the mass of the objects and the closer they are to each other, the greater the force of gravitational attraction between them.
The formula of the universal law of gravitation:
The mathematical formula to calculate the gravitational force between two objects is expressed as follows:
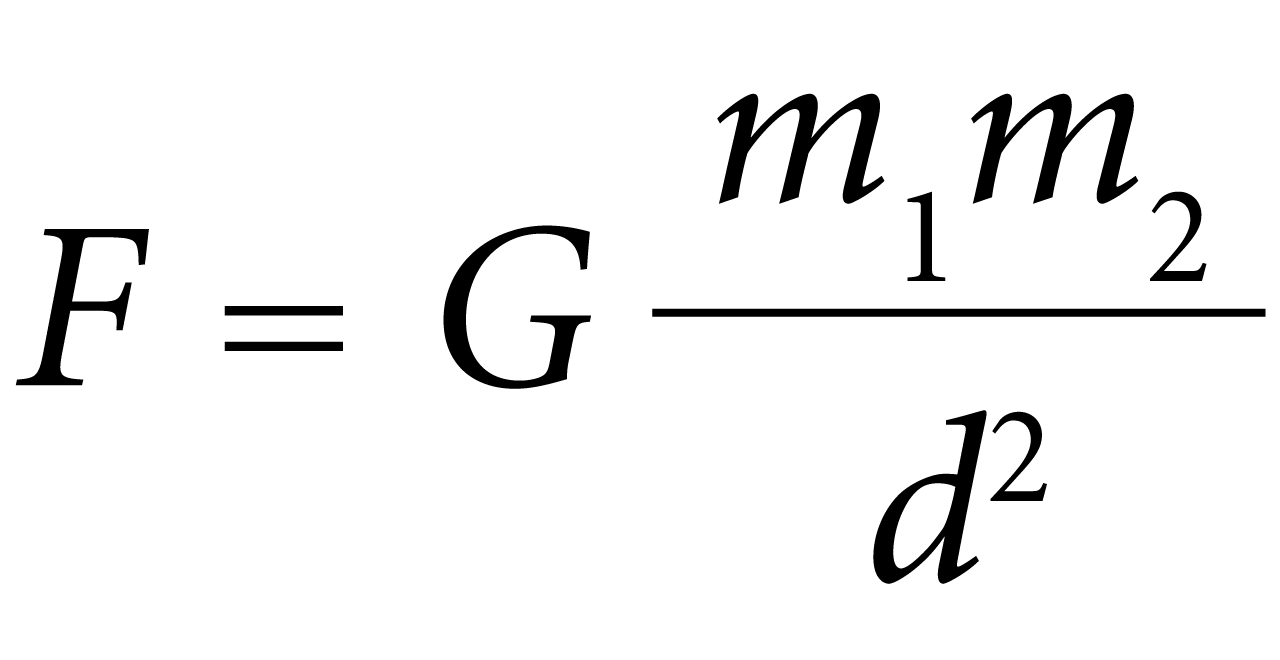
Where:
-
F is the gravitational force between objects expressed in newtons,
-
G is the universal gravitational constant, approximately 6.674 × 10 -11 N (m/kg) 2
-
m 1 and m 2 are the masses of the objects expressed in kilograms (kg).
-
r is the distance between the centers of mass of objects expressed in meters (m).
The universal gravitational constant (G) has a value of approximately 6.674 × 10 -11 N (m/kg) 2 and is used to scale the force of attraction as a function of the units of mass and distance used.
Importance of the universal law of gravitation:
The universal law of gravitation is of the utmost importance in the study and understanding of the universe. Through this law, we can explain and predict phenomena such as the orbit of the planets around the Sun, the movements of the moons around the planets, and the interaction between massive objects in space.
In addition, the law also has practical applications in everyday life. For example, it allows understanding the operation of artificial satellites that orbit the Earth and is essential for space navigation and the planning of space missions.
Examples of the application of the universal law of gravitation:
Below we show 4 examples in which Newton's universal law of gravitation is applied:
1. Earth's orbit around the Sun
The gravitational force between the Earth and the Sun is responsible for keeping our planet in a stable orbit around the star.
This force allows the Earth to keep in circular motion around the Sun and determines the period of one year. The force that the Sun exerts on the Earth is perpendicular to the linear velocity of the Earth at each moment.
2. The Moon and the tides
The gravitational force between the Earth and the Moon is responsible for the tides. The Moon exerts an attractive force on the oceans, causing the water level to rise and fall as the Earth rotates.
Like the Sun and the Earth, this force is the centripetal force that forces the Moon to orbit the Earth.
3. Artificial satellites
In the design and operation of artificial satellites, calculations are also made using the formula of the universal law of gravitation.
To keep a satellite in orbit, a specific speed and altitude is needed to balance the gravitational force with the centrifugal force generated by orbital motion.
4. Falling objects
The law also applies to falling objects on the Earth's surface. The greater the mass of the object, the greater the gravitational force acting on it and the faster it will fall.
Exercises of the universal law of gravitation
Below we show three solved exercises that illustrate the application of this law of physics:
Exercise 1: Calculating the gravitational force between two bodies
Suppose we have two objects: one with a mass of 5 kg and the other with a mass of 8 kg. The distance between the centers of mass of the objects is 2 meters. We want to calculate the gravitational force between them.
Data
-
m 1 = 5kg
-
m 2 = 8kg
-
r=2m
-
G = 6.674 × 10 -11 N (m/kg) 2
Solution:
We use the formula of the universal law of gravitation:
F = G (m1 · m2 ) / r2
Substituting the known values:
F = (6.674 × 10-11 N (m/kg)2 ) * (5 kg * 8 kg) / (2 m)2
F = 6.674 × 10-10 N
Therefore, the gravitational force between the two bodies is approximately 6.674 × 10-10 N.
Exercise 2: Calculating the gravitational force between the Earth and an object
Suppose we want to calculate the gravitational force between the Earth (mass ≈ 5.972 × 1024 kg) and an object with a mass of 100 kg. The distance between the center of the Earth and the object is 6.371 × 106 meters (approximate radius of the Earth).
Data:
-
m1 (mass of the Earth) = 5.972 × 1024 kg
-
m2 (mass of the object) = 100 kg
-
r (distance) = 6.371 × 106 m
-
G = 6.674 × 10-11 N (m/kg)2
Solution:
We apply the formula of the universal law of gravitation:
F = G (m1 · m2 ) / r2
Substituting the known values:
F = (6.674 × 10-11 N (m/kg) 2 ) * ((5.972 × 1024 kg) * (100 kg)) / (6.371 × 106 m)2
F = 981.95N
Therefore, the gravitational force between the Earth and the object is approximately 981.95 N.
Exercise 3: Calculating the mass of an object from the gravitational force
Suppose we have two objects, and we know that the gravitational force between them is 100 N. The distance between the objects is 10 meters and the mass of one of the objects is 5 kg. We want to calculate the mass of the second object.
Data:
-
F = 100N
-
r = 10m
-
m 1 = 5kg
-
G = 6.674 × 10-11 N (m/kg)2
Solution:
We use the formula of the universal law of gravitation and clear m2:
F = G (m1 · m2 ) / r2
We clear m2:
m2 = (F * r2 ) / (G * m1 )
Substituting the known values:
m2 = (100 N * (10 m)2 ) / ((6.674 × 10-11 N (m/kg)2 ) * 5 kg)
m2 ≈ 2.997 × 1013 kg
Therefore, the mass of the second object is approximately 2.997 × 1013 kg.